BĐT

Đề bài: (Câu 5b đề thi học kỳ II môn Toán 8 - THPT Chuyên Hà Nội Amsterdam)
Cho các số thực dương $x,y,z$ thỏa mãn $xyz=1$.
Chứng minh rằng: $\dfrac{{{x^2}{y^2}}}{{2{x^2} + {y^2} + 3{x^2}{y^2}}} + \dfrac{{{y^2}{z^2}}}{{2{y^2} + {z^2} + 3{y^2}{z^2}}} + \dfrac{{{z^2}{x^2}}}{{2{z^2} + {x^2} + 3{z^2}{x^2}}} \le \dfrac{1}{2} (\bigstar)$
Giải:

BĐT

Đề bài: (Câu hỏi của bạn Hoàng Đăng Đức hỏi trên facebook Trợ Giúp Toán Học)
Cho $a,b,c>0$, chứng minh rằng: $\sqrt {\dfrac{a}{{b + c + 2a}}}  + \sqrt {\dfrac{b}{{a + c + 2b}}}  + \sqrt {\dfrac{c}{{b + a + 2c}}}  \le \dfrac{3}{2} (\bigstar)$
Giải:

BĐT

Đề bài: (Câu 5b đề thi học kỳ II toán 10 - THPT Chuyên Hà Nội Amsterdam)
Cho các số thực dương $x,y,z$ thỏa mãn $xy+yz+zx=3$.
Tìm giá trị nhỏ nhất của biểu thức: $P = \dfrac{{yz}}{{{x^3} + 2}} + \dfrac{{zx}}{{{y^3} + 2}} + \dfrac{{xy}}{{{z^3} + 2}}$
Giải:

BĐT

Đề bài: (Câu hỏi của bạn Hoàng Thanh Thúy hỏi trên facebook Trợ Giúp Toán Học)
Cho các số thực dương $x,y,z$ thỏa mãn $x+y+z=3$.
Chứng minh rằng: $\dfrac{x}{{x + \sqrt {3x + yz} }} + \dfrac{y}{{y + \sqrt {3y + zx} }} + \dfrac{z}{{z + \sqrt {3z + xy} }} \le 1 (\bigstar)$
Giải:

HPT

Đề bài: (TRÍCH CÂU 9 ĐỀ KHẢO SÁT CHẤT LƯỢNG TOÁN 12 SỞ GD&ĐT HÀ NỘI)
Giải hệ phương trình: $\left\{ \begin{array}{l} \sqrt {{x^2}\left( {1 + {y^2}} \right)} - \sqrt {1 + {x^2}} = 1 - xy\\ \left( {2x - 7xy} \right)\left( {\sqrt {3x - 2} - \sqrt {x + 3xy} } \right) = 5 \end{array} \right.$
Giải:

Oxy

Đề bài: (TRÍCH CÂU 8 ĐỀ KHẢO SÁT CHẤT LƯỢNG TOÁN 12 SỞ GD&ĐT HÀ NỘI 04/2016)
Trong mặt phẳng với hệ toạ độ $Oxy$, cho $\Delta{ABC}$ vuông tại $A$. Gọi $H(5;5)$ là hình chiếu vuông góc của $A$ lên $BC$, đường phân giác trong góc $A$ của $\Delta{ABC}$ nằm trên đường thẳng $x-7y+20=0.$ Đường thẳng chứa trung tuyến $AM$ của $\Delta{ABC}$ đi qua điểm $K(-10;5)$. Tìm tọa độ các đỉnh của $\Delta{ABC}$, biết điểm $B$ có tung độ dương.
Giải:

BĐT hay.

Đề bài: (Một bài bất đẳng thức hay)
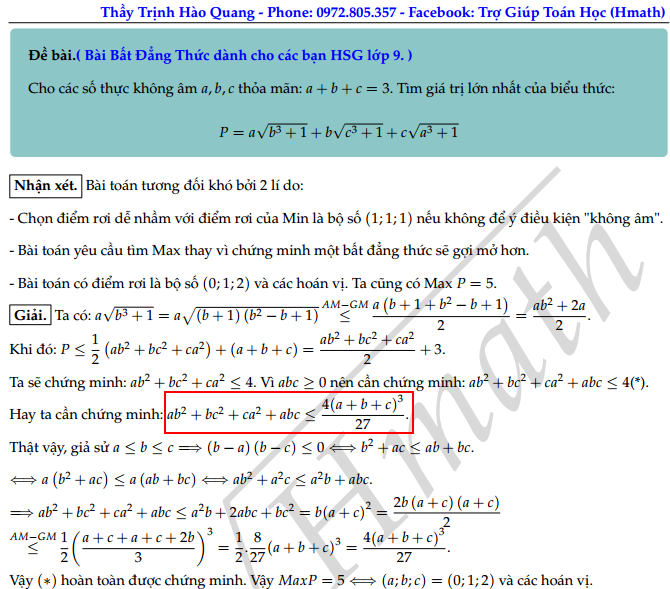
Cho các số thực không âm $a,b,c$ thỏa mãn: $a+b+c=3$. Tìm giá trị lớn nhất của biểu thức:
$P = a\sqrt {{b^3} + 1}  + b\sqrt {{c^3} + 1}  + c\sqrt {{a^3} + 1}$
Giải: