GPT

Đề bài. (Câu hỏi của bạn Chanh Lemonade hỏi trên facebook Trợ Giúp Toán Học)
Cho $a,b,c$ là các số thực đôi một khác nhau.
Giải phương trình: $\dfrac{{\left( {b - c} \right)\left( {1 + {a^2}} \right)}}{{x + {a^2}}} + \dfrac{{\left( {c - a} \right)\left( {1 + {b^2}} \right)}}{{x + {b^2}}} + \dfrac{{\left( {a - b} \right)\left( {1 + {c^2}} \right)}}{{x + {c^2}}} = 0$
Giải:

Vẻ đẹp bề ngoài không quan trọng, tâm hồn mới là quý giá

Đề bài: (Câu hỏi của bạn Phạm Văn Minh hỏi trên facebook Trợ Giúp Toán Học)
Cho các số thực không âm $a,b,c$ thỏa mãn $a+b+c=3$.
Tìm giá trị LỚN nhất của biểu thức: ${P = \sqrt {ab}  + \sqrt {bc}  + 2\sqrt {ca} }$
Giải:

Ba cách khác nhau cho một bài BĐT.

Đề bài: (Câu hỏi của bạn Kim Ngân hỏi trên facebook Trợ Giúp Toán Học)
Cho các số thực dương $a,b$. Chứng minh rằng: ${\dfrac{{a + b}}{{\sqrt {a\left( {3a + b} \right)}  + \sqrt {b\left( {3b + a} \right)} }} \ge \dfrac{1}{2}}$
Giải:

THPT QG 2016

HPT

Đề bài: (Câu hỏi của bạn Võ Đức hỏi trên facebook Trợ Giúp Toán Học)
Giải hệ phương trình $\left\{ \begin{array}{l} y\sqrt {{x^4} + 2{x^2}} + \sqrt {1 - 2y} = 0\\ \sqrt {\left( {2xy - 1} \right)\left( {xy + y} \right)} - \left( {x + 4} \right)y = 1 \end{array} \right.$
Giải:

BĐT

Đề bài: (Câu hỏi của bạn Lý Học Đông hỏi trên faccebook Trợ Giúp Toán Học)
Cho các số thực dương $a,b,c$ thỏa mãn: $a+b+c=1$. Tìm giá trị nhỏ nhất của biểu thức:
$A = 14\left( {{a^2} + {b^2} + {c^2}} \right) + \dfrac{{ab + bc + ca}}{{{a^2}b + {b^2}c + {c^2}a}}$.
Giải:

BĐT

Đề bài: (Câu 5b đề thi học kỳ II môn Toán 8 - THPT Chuyên Hà Nội Amsterdam)
Cho các số thực dương $x,y,z$ thỏa mãn $xyz=1$.
Chứng minh rằng: $\dfrac{{{x^2}{y^2}}}{{2{x^2} + {y^2} + 3{x^2}{y^2}}} + \dfrac{{{y^2}{z^2}}}{{2{y^2} + {z^2} + 3{y^2}{z^2}}} + \dfrac{{{z^2}{x^2}}}{{2{z^2} + {x^2} + 3{z^2}{x^2}}} \le \dfrac{1}{2} (\bigstar)$
Giải:

BĐT

Đề bài: (Câu hỏi của bạn Hoàng Đăng Đức hỏi trên facebook Trợ Giúp Toán Học)
Cho $a,b,c>0$, chứng minh rằng: $\sqrt {\dfrac{a}{{b + c + 2a}}}  + \sqrt {\dfrac{b}{{a + c + 2b}}}  + \sqrt {\dfrac{c}{{b + a + 2c}}}  \le \dfrac{3}{2} (\bigstar)$
Giải:

BĐT

Đề bài: (Câu 5b đề thi học kỳ II toán 10 - THPT Chuyên Hà Nội Amsterdam)
Cho các số thực dương $x,y,z$ thỏa mãn $xy+yz+zx=3$.
Tìm giá trị nhỏ nhất của biểu thức: $P = \dfrac{{yz}}{{{x^3} + 2}} + \dfrac{{zx}}{{{y^3} + 2}} + \dfrac{{xy}}{{{z^3} + 2}}$
Giải:

BĐT

Đề bài: (Câu hỏi của bạn Hoàng Thanh Thúy hỏi trên facebook Trợ Giúp Toán Học)
Cho các số thực dương $x,y,z$ thỏa mãn $x+y+z=3$.
Chứng minh rằng: $\dfrac{x}{{x + \sqrt {3x + yz} }} + \dfrac{y}{{y + \sqrt {3y + zx} }} + \dfrac{z}{{z + \sqrt {3z + xy} }} \le 1 (\bigstar)$
Giải:

HPT

Đề bài: (TRÍCH CÂU 9 ĐỀ KHẢO SÁT CHẤT LƯỢNG TOÁN 12 SỞ GD&ĐT HÀ NỘI)
Giải hệ phương trình: $\left\{ \begin{array}{l} \sqrt {{x^2}\left( {1 + {y^2}} \right)} - \sqrt {1 + {x^2}} = 1 - xy\\ \left( {2x - 7xy} \right)\left( {\sqrt {3x - 2} - \sqrt {x + 3xy} } \right) = 5 \end{array} \right.$
Giải:

Oxy

Đề bài: (TRÍCH CÂU 8 ĐỀ KHẢO SÁT CHẤT LƯỢNG TOÁN 12 SỞ GD&ĐT HÀ NỘI 04/2016)
Trong mặt phẳng với hệ toạ độ $Oxy$, cho $\Delta{ABC}$ vuông tại $A$. Gọi $H(5;5)$ là hình chiếu vuông góc của $A$ lên $BC$, đường phân giác trong góc $A$ của $\Delta{ABC}$ nằm trên đường thẳng $x-7y+20=0.$ Đường thẳng chứa trung tuyến $AM$ của $\Delta{ABC}$ đi qua điểm $K(-10;5)$. Tìm tọa độ các đỉnh của $\Delta{ABC}$, biết điểm $B$ có tung độ dương.
Giải:

BĐT hay.

Đề bài: (Một bài bất đẳng thức hay)
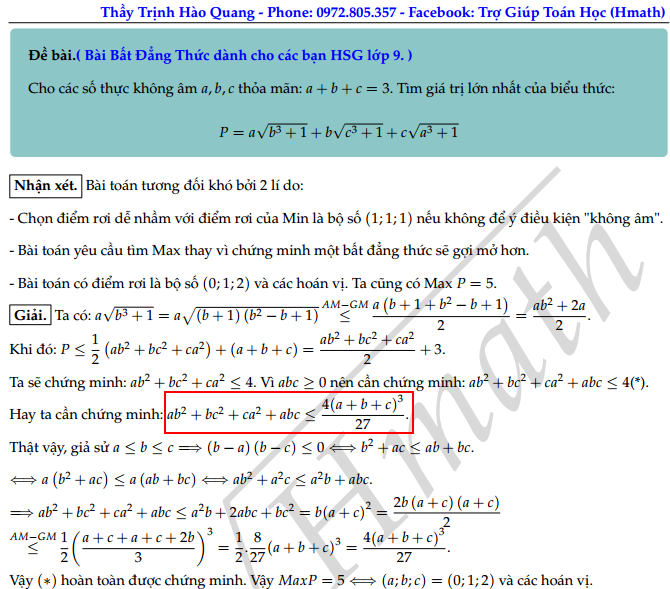
Cho các số thực không âm $a,b,c$ thỏa mãn: $a+b+c=3$. Tìm giá trị lớn nhất của biểu thức:
$P = a\sqrt {{b^3} + 1}  + b\sqrt {{c^3} + 1}  + c\sqrt {{a^3} + 1}$
Giải:

HPT

Đề bài: (Câu hỏi của bạn Mất Trí Nhớ hỏi trên facebook Trợ Giúp Toán Học)
Giải hệ phương trình: $\left\{ \begin{array}{l} {x^2} + 2x - 2 = \sqrt { - {y^2} - 4y - 2} \\ 6x - y - 11 + \sqrt {10 - 4x - 2{x^2}}  = 0 \end{array} \right.$
Giải:

BĐT

Đề bài: (Câu hỏi của bạn Nguyễn Hồng Quân hỏi trên facebook Trợ Giúp Toán Học)
Cho các số thực dương $a,b,c$ thỏa mãn: ${a^2}{b^2} + {b^2}{c^2} + 1 \le 3b.$
Tìm giá trị nhỏ nhất của biểu thức: $P = \dfrac{1}{{{{\left( {a + 1} \right)}^2}}} + \dfrac{{4{b^2}}}{{{{\left( {1 + 2b} \right)}^2}}} + \dfrac{8}{{{{\left( {c + 3} \right)}^2}}}$.
Giải:

BĐT

Đề bài: (Câu hỏi của bạn Hà Huy Hoàng hỏi trên facebook Trợ Giúp Toán Học)
Cho các số thực dương $x,y,z$ thỏa mãn: $\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{2}{z}.$\
Tìm giá trị nhỏ nhất của biểu thức: $T = \dfrac{{x + z}}{{2x - z}} + \dfrac{{y + z}}{{2y - z}}$.
Giải:

BĐT

Đề bài: (Câu hỏi của bạn Trang Nguyen đăng trên facebook Trợ Giúp Toán Học)
Cho các số thực dương $x,y,z$ thỏa mãn: $\left( {x + y} \right)\left( {y + z} \right)\left( {z + x} \right) = 1.$
Chứng minh rằng: $\dfrac{{\sqrt {{x^2} + xy + {y^2}} }}{{\sqrt {xy} + 1}} + \dfrac{{\sqrt {{y^2} + yz + {z^2}} }}{{\sqrt {yz} + 1}} + \dfrac{{\sqrt {{z^2} + zx + {x^2}} }}{{\sqrt {zx} + 1}} \ge \sqrt 3 (\bigstar).$
Giải:

Dãy số.

Đề bài: (Câu hỏi của bạn Dieu Linh Tran hỏi trên facebook Trợ Giúp Toán Học)
Cho dãy số $(u_n)$ được xác định bởi: $\left\{ \begin{array}{l} {u_1} = {u_2} = 0\\ {u_{n + 1}} = \dfrac{{u_n^2 + 2{u_n} - {u_{n - 1}} + 2}}{{{u_{n - 1}} + 1}}\left( {n \ge 2} \right) \end{array} \right.$
Chứng minh rằng: $u_n$ nguyên với mọi $n.$
Giải:

BĐT

Đề bài: (Câu bất đẳng thức trích trong đề thi HSG Toán 9 - Quận Hoàn Kiếm - Hà Nội)
Cho $\Delta{ABC}$ vuông tại $A,$ có độ dài các cạnh $BC=a, CA=b, AB=c.$ Tìm giá trị nhỏ nhất của biểu thức:
$M = 8{a^2}\left( {\dfrac{1}{{{b^2}}} + \dfrac{1}{{{c^2}}}} \right) + \dfrac{{b + c}}{a} + 2016$
Giải:

HHP

Đề bài: (Câu hỏi của thầy Vũ Ngọc Hòa hỏi trên facebook Trợ Giúp Toán Học)
Cho $\Delta{ABC}$ vuông tại $A,$ có $AH$ là đường cao. $M$ là điểm tùy ý thuộc đoạn $AH(M \neq A,H).$ Gọi $P$ là điểm thuộc $BM$ kéo dài sao cho $CP=CA$ và $Q$ là điểm thuộc $CM$ kéo dài sao cho $BQ=BA, CP \cap BQ = E.$ Chứng minh rằng: $EP=EQ.$
Giải:

BPT

Đề bài: (Câu hỏi của bạn Mưa Con Đường hỏi trên facebook Trợ Giúp Toán Học)
Giải bất phương trình: $4\left( {3x + \sqrt {9{x^2} - 4} } \right) > \dfrac{1}{x} + \dfrac{{9x}}{{{x^2} + 1}}(\bigstar)$
Giải:

BĐT

Đề bài: (Câu hỏi của bạn Mèo Gay Lọ hỏi trên facebook Trợ Giúp Toán Học)
Cho trước hai số thực $a,b$. Tìm giá trị nhỏ nhất của biểu thức sau với $x,y,z$ là các số thực dương tùy ý: $P = \dfrac{{{x^2}}}{{\left( {ay + bz} \right)\left( {az + by} \right)}} + \dfrac{{{y^2}}}{{\left( {az + bx} \right)\left( {ax + bz} \right)}} + \dfrac{{{z^2}}}{{\left( {ax + by} \right)\left( {ay + bz} \right)}}$
Giải:

BĐT

Đề bài: (Câu hỏi của bạn Cần Một Bờ Vai hỏi trên facebook Trợ Giúp Toán Học)
Bài 01: Cho $a,b,c$ là ba số thực dương. CMR: $\dfrac{a}{{\sqrt {{a^2} + 8bc} }} + \dfrac{b}{{\sqrt {{b^2} + 8ca} }} + \dfrac{c}{{\sqrt {{c^2} + 8ab} }} \ge 1(\bigstar)$
Bài 02: Cho $a,b,c$ là ba số thực dương thỏa mãn $abc=1$.
CMR: $\left( {a + b} \right)\left( {b + c} \right)\left( {c + a} \right) \ge 2\left( {1 + a + b + c} \right)(\clubsuit)$
Giải: