Đề bài: (Câu hỏi của bạn Nhẫn Trí Đạt hỏi trên facebook Trợ Giúp Toán Học)
Chứng minh rằng: Hàm số$y = f\left( x \right) = \sqrt {\left| x \right|}$ không tồn tại đạo hàm tại x=0 nhưng đạt Cực tiểu tại đó.
Giải:
Bài toán sẽ gây phiền toái cho rất nhiều bạn, mặc dù nó áp dụng kiến thức rất căn bản trong SGK.
Tôi cá rằng nhiều giáo viên luyện thi ĐH cũng sẽ loay hoay bài này vì nó không phải là kiến thức thi ĐH.
a) Chứng minh: Không tồn tại đạo hàm tại x=0.
Xét $f'\left( 0 \right) = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{f\left( {\Delta x + 0} \right) - f\left( 0 \right)}}{{\Delta x}} = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{\sqrt {\left| {\Delta x} \right|} }}{{\Delta x}}.$
------Cứ mỗi giáo viên tha hóa biến chất thì đâu đó vẫn có những con người tận tâm tận lực và hết lòng vì học sinh------==============Bị chối bỏ, Tôi quyết tâm trở thành người thầy mà tôi chưa bao giờ có được!==============
Lịch sử các nhà toán học
Thứ Bảy, 30 tháng 8, 2014
Biến đổi để đưa về xét HÀM.
Đề bài: (Câu hỏi của bạn Tịnh Dương hỏi trên facebook Trợ Giúp Toán Học)
Giải hệ phương trình: $\left\{ {\begin{array}{*{20}{l}}
{4{x^3} - 3x + \left( {y - 1} \right)\sqrt {2y + 1} = 0}\\
{2{x^2} + x + \sqrt { - y\left( {2y + 1} \right)} = 0}
\end{array}} \right.$
Giải:
Điều kiện: $-\frac{1}{2}\le x,y\le 0$
Đọc tiếp
Giải hệ phương trình: $\left\{ {\begin{array}{*{20}{l}}
{4{x^3} - 3x + \left( {y - 1} \right)\sqrt {2y + 1} = 0}\\
{2{x^2} + x + \sqrt { - y\left( {2y + 1} \right)} = 0}
\end{array}} \right.$
Giải:
Điều kiện: $-\frac{1}{2}\le x,y\le 0$
$4{{x}^{3}}-3x=-4.\frac{2y+1}{4}\sqrt{\frac{2y+1}{4}}-\left( -3\sqrt{\frac{2y+1}{4}} \right)\Leftrightarrow 4{{x}^{3}}-3x=4{{\left( -\sqrt{\frac{2y+1}{4}} \right)}^{3}}-\left( -3\sqrt{\frac{2y+1}{4}} \right)$
Thứ Sáu, 29 tháng 8, 2014
MÒ để CÓ CĂN CỨ.
Đề bài: (Câu hỏi của bạn Milky Way hỏi trên facebook Trợ Giúp Toán Học)
Giải hệ phương trình sau:$\left\{ \begin{array}{l}
{x^3} - {x^2} + 3x = {y^3} + {y^2} + 3\\
\left( {x + 1} \right)\left( {y + 2} \right) = 4
\end{array} \right.$
Giải:
Nhìn vào HPT chúng ta nghĩ ngay đến phép thế, khổ nỗi thứ từ PT2 vào PT1 ta sẽ nhận được PT phức tạp hơn và cũng không có điều kiện của x hay y để nghĩ đến việc xét hàm từ PT phức tạp này.
Khi giải HPT hay PT vô tỷ chúng ta cũng hay nhẩm nghiệm bằng tay hoặc bằng máy tính Casio.
Ở đây cũng vậy chúng ta nhẩm thấy HPT có 2 nghiệm đẹp là (1;0) và (-3;-4). Ta sẽ lập PT đường thẳng đi qua 2 điểm này là: y=x-1 hay x-y-1=0. Khi đó chúng ta cố gắng đưa HPT về đẳng thức xuất hiện một nhân tử là (x-y-1) và ta có cách giải sau đây:
Đọc tiếp
Giải hệ phương trình sau:$\left\{ \begin{array}{l}
{x^3} - {x^2} + 3x = {y^3} + {y^2} + 3\\
\left( {x + 1} \right)\left( {y + 2} \right) = 4
\end{array} \right.$
Giải:
Nhìn vào HPT chúng ta nghĩ ngay đến phép thế, khổ nỗi thứ từ PT2 vào PT1 ta sẽ nhận được PT phức tạp hơn và cũng không có điều kiện của x hay y để nghĩ đến việc xét hàm từ PT phức tạp này.
Khi giải HPT hay PT vô tỷ chúng ta cũng hay nhẩm nghiệm bằng tay hoặc bằng máy tính Casio.
Ở đây cũng vậy chúng ta nhẩm thấy HPT có 2 nghiệm đẹp là (1;0) và (-3;-4). Ta sẽ lập PT đường thẳng đi qua 2 điểm này là: y=x-1 hay x-y-1=0. Khi đó chúng ta cố gắng đưa HPT về đẳng thức xuất hiện một nhân tử là (x-y-1) và ta có cách giải sau đây:
Thứ Năm, 28 tháng 8, 2014
BI ẨN TUYỆT ĐẸP qua một bài toán tổng quát.
Đề bài: (Câu hỏi của bạn Hiếu Minh Nguyễn hỏi trên facebook Trợ Giúp Toán Học)
Xác định dạng của tâm giác ABC biết rằng:$\frac{{cosA}}{3} + \frac{{cos\,B}}{4} + \frac{{cos\,C}}{5} = \frac{5}{{12}}.$
Giải:
Đây là một bài toán rất hay, trước khi có tính nhất này ta sẽ thấy xuất hiện một đẳng thức rất đẹp liên quan đến bộ số Pitago (3,4,5). Nhưng trước hết thầy phát biểu vầ chứng minh một bài toán tổng quát hơn như sau:
$CMR:{x^2} + {y^2} + {z^2} \ge 2xy\,\cos C + 2yz\,cos\,A + 2zx\,cos\,B\left( * \right)\,.\,\forall \Delta ABC\& x,y,z \in R.$Thật vậy:
Đọc tiếp
Xác định dạng của tâm giác ABC biết rằng:$\frac{{cosA}}{3} + \frac{{cos\,B}}{4} + \frac{{cos\,C}}{5} = \frac{5}{{12}}.$
Giải:
Đây là một bài toán rất hay, trước khi có tính nhất này ta sẽ thấy xuất hiện một đẳng thức rất đẹp liên quan đến bộ số Pitago (3,4,5). Nhưng trước hết thầy phát biểu vầ chứng minh một bài toán tổng quát hơn như sau:
$CMR:{x^2} + {y^2} + {z^2} \ge 2xy\,\cos C + 2yz\,cos\,A + 2zx\,cos\,B\left( * \right)\,.\,\forall \Delta ABC\& x,y,z \in R.$Thật vậy:
Thứ Tư, 27 tháng 8, 2014
CT tỉ số trong hình không gian.
Đề bài: (Câu hỏi của bạn Dương Minh hỏi trên facebook Trợ Giúp Toán Học)
Cho hình chóp S.ABC, gọi G là trọng tâm của đáy ABC. Một mặt phẳng (P) lưu động cắt 3 cạnh bên tại A', B', C' và cắt SG tại G'. Chứng minh rằng:$\frac{{SA}}{{SA'}} + \frac{{SB}}{{SB'}} + \frac{{SC}}{{SC'}} = \frac{{3SG}}{{SG'}}.$
Giải:
Gọi M và M' lần lượt là trung điểm của BC và B'C' ta thấy:
Đọc tiếp
Cho hình chóp S.ABC, gọi G là trọng tâm của đáy ABC. Một mặt phẳng (P) lưu động cắt 3 cạnh bên tại A', B', C' và cắt SG tại G'. Chứng minh rằng:$\frac{{SA}}{{SA'}} + \frac{{SB}}{{SB'}} + \frac{{SC}}{{SC'}} = \frac{{3SG}}{{SG'}}.$
Giải:
Gọi M và M' lần lượt là trung điểm của BC và B'C' ta thấy:
Thứ Hai, 25 tháng 8, 2014
"Ép" cái KHÓ về cái DỄ.
Đề bài: (Câu hỏi của bạn Thanh Tung hỏi trên facebook Trợ Giúp Toán Học)
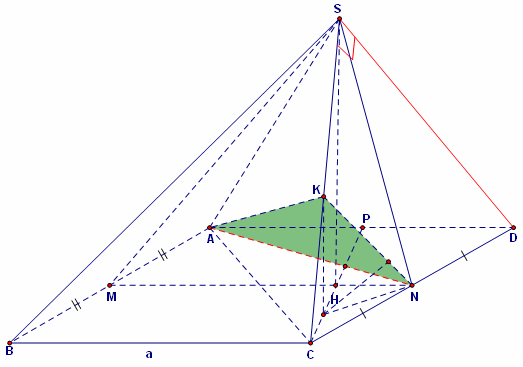
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Tam giác SAB đều. Tam giác SCD vuông cân tại S. N là trung điểm của cạnh CD.
a/ Tính thể tích hình chóp S.ABCD.
b/ Tính khoảng cách AN tới SD.
Giải:
MN \bot CD\\
SN \bot CD
\end{array} \right. \Rightarrow CD \bot \left( {SMN} \right).$
Trong (SMN), dựng SH vuông góc MN ta có:$SH \bot \left( {ABCD} \right).$
$SM = \frac{{a\sqrt 3 }}{2};MN = a;SN = \frac{a}{2} \Rightarrow M{N^2} = A{M^2} + S{N^2}.$
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Tam giác SAB đều. Tam giác SCD vuông cân tại S. N là trung điểm của cạnh CD.
a/ Tính thể tích hình chóp S.ABCD.
b/ Tính khoảng cách AN tới SD.
Giải:
Một bài toán khá hay nếu sử dụng công cụ hình học thuần túy.
a) Gọi M là trung điểm của AB ta có:$\left\{ \begin{array}{l}MN \bot CD\\
SN \bot CD
\end{array} \right. \Rightarrow CD \bot \left( {SMN} \right).$
Trong (SMN), dựng SH vuông góc MN ta có:$SH \bot \left( {ABCD} \right).$
$SM = \frac{{a\sqrt 3 }}{2};MN = a;SN = \frac{a}{2} \Rightarrow M{N^2} = A{M^2} + S{N^2}.$
Chủ Nhật, 24 tháng 8, 2014
Mỗi ngày một tính chất Oxy.
Đề bài: (Câu hỏi của bạn Nguyễn Văn Dư hỏi trên facebook Trợ Giúp Toán Học)
Cho tam giác ABC vuông tai A, 2 điểm B,C đối xứng nhau qua gốc tọa độ. Phương trình đường phân giác góc trong góc B là d:x+2y-5=0 và điểm K(6;2) thuộc AC. Tìm tọa độ các đỉnh A B C?
Giải:
Gọi D là điểm đối xứng với O qua phân giác d khi đó ta dễ chứng minh được D thuộc AB.
$\begin{array}{l}
Coi\,D\left( {a;b} \right) \Rightarrow \left\{ \begin{array}{l}
\overrightarrow {OD} .{\overrightarrow u _d} = 0\left( {OD \bot d} \right)\\
M\left( {\frac{a}{2};\frac{b}{2}} \right) \in d
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
a + 2b = 10\\
2a - b = 0
\end{array} \right. \Leftrightarrow D\left( {2;4} \right)\\
Coi\,B\left( {5 - 2b;b} \right) \in d \Rightarrow C\left( {2b - 5; - b} \right)\\
\Rightarrow \left\{ \begin{array}{l}
\overrightarrow {KC} = \left( {2b - 11; - b - 2} \right)\\
\overrightarrow {DB} = \left( {3 - 2b;b - 4} \right)
\end{array} \right.\\
Do\,\left\{ \begin{array}{l}
KC \equiv AC,\,DB \equiv AB\\
AB \bot AC
\end{array} \right. \Rightarrow DB \bot KC\\
\Leftrightarrow \overrightarrow {DB} .\overrightarrow {KC} = 0 \Leftrightarrow {b^2} - 6b + 5 = 0 \Leftrightarrow \left[ \begin{array}{l}
b = 1\\
b = 5
\end{array} \right.
\end{array}.$
Đọc tiếp
Cho tam giác ABC vuông tai A, 2 điểm B,C đối xứng nhau qua gốc tọa độ. Phương trình đường phân giác góc trong góc B là d:x+2y-5=0 và điểm K(6;2) thuộc AC. Tìm tọa độ các đỉnh A B C?
Giải:
Gọi D là điểm đối xứng với O qua phân giác d khi đó ta dễ chứng minh được D thuộc AB.
$\begin{array}{l}
Coi\,D\left( {a;b} \right) \Rightarrow \left\{ \begin{array}{l}
\overrightarrow {OD} .{\overrightarrow u _d} = 0\left( {OD \bot d} \right)\\
M\left( {\frac{a}{2};\frac{b}{2}} \right) \in d
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
a + 2b = 10\\
2a - b = 0
\end{array} \right. \Leftrightarrow D\left( {2;4} \right)\\
Coi\,B\left( {5 - 2b;b} \right) \in d \Rightarrow C\left( {2b - 5; - b} \right)\\
\Rightarrow \left\{ \begin{array}{l}
\overrightarrow {KC} = \left( {2b - 11; - b - 2} \right)\\
\overrightarrow {DB} = \left( {3 - 2b;b - 4} \right)
\end{array} \right.\\
Do\,\left\{ \begin{array}{l}
KC \equiv AC,\,DB \equiv AB\\
AB \bot AC
\end{array} \right. \Rightarrow DB \bot KC\\
\Leftrightarrow \overrightarrow {DB} .\overrightarrow {KC} = 0 \Leftrightarrow {b^2} - 6b + 5 = 0 \Leftrightarrow \left[ \begin{array}{l}
b = 1\\
b = 5
\end{array} \right.
\end{array}.$
Thứ Sáu, 22 tháng 8, 2014
6 cái HAY không may 1 cái DỞ...
Trước khi nói về một cái DỞ, tôi mời các bạn "thưởng thức" lá thư của vị Hiệu trưởng trường THPT Lương Thế Vinh - Hà Nội. Có lẽ quý vị cũng đoán ra vị này là ai rồi phải không? Ông thường xuất hiện mỗi khi báo chí cần ông cho ý kiến về một chính xác đổi mới trong Giáo Dục nào đó. Và...Đó là người thầy của thầy tôi - Giáo sư Văn Như Cương...
Lá thư rất hay nhưng có phần giống version "Xin thầy hãy dạy con tôi..." của Tổng Thống Mỹ A.Lincoln gửi thầy Hiệu trưởng nơi con trai ông theo học.
Gọi là 6 cái HAY nhưng tiềm ẩn trong mỗi cái HAY vẫn ẩn chứa mục đích lầm thương hiệu của Giáo sư...
Lá thư gửi các bậc cha mẹ học sinh trường Lương Thế Vinh có nội dung như sau:
Mỗi ngày một tính chất hình Oxy.
Đề bài: (Câu hỏi của bạn Lê Hiếu hỏi trên facebook Trợ Giúp Toán Học)
Trong mặt phẳng Oxy cho hình thang ABCD vuông tại A và D có AB=AD<CD, điểm B(1,2), đường thẳng BD có phương trình y=2. Biết đường thẳng (d): 7x-y-25=0 cắt các đoạn thẳng AD, CD lần lượt tại hai điểm M, N sao cho BM vuông góc với BC và tia BN là tia phân giác của góc MBC. Tìm điểm D có hoành độ dương.
Giải:
Gọi H và K lần lượt là chân đường cao hạ từ
B xuống DC và MN. Ta có:
Đọc tiếp
Trong mặt phẳng Oxy cho hình thang ABCD vuông tại A và D có AB=AD<CD, điểm B(1,2), đường thẳng BD có phương trình y=2. Biết đường thẳng (d): 7x-y-25=0 cắt các đoạn thẳng AD, CD lần lượt tại hai điểm M, N sao cho BM vuông góc với BC và tia BN là tia phân giác của góc MBC. Tìm điểm D có hoành độ dương.
Giải:
Gọi H và K lần lượt là chân đường cao hạ từ
B xuống DC và MN. Ta có:
Sử dụng PP ĐỔI ĐIỂM nhiều lần để tính khoảng cách từ điểm đến mặt.
Đề bài: (Câu hỏi của cô Phạm Thiên Lý và gợi ý của thầy Ngô Nghiệp trên facebook Trợ Giúp Toán Học)
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 2a. SA vuông góc với đáy ABC và SA=a. Gọi M và E lần lượt là trung điểm của SC và AB. Tính khoảng cách từ điểm S đến mặt phẳng (MAB).
Giải:
Bài toán hoàn toàn được giải quyết nhanh gọn nếu các bạn học sinh mà cô Lý đang dạy đã học lớp 12.
Vì khi đó chúng ta còn 2 công cụ là ĐỔI ĐỈNH (Có ứng dụng tỉ số thể tích) và GẮN TOẠ ĐỘ OXYZ.
Nhưng do học sinh đang học 11 nên ta chỉ có thể dùng PP ĐỔI ĐIỂM như sau:
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 2a. SA vuông góc với đáy ABC và SA=a. Gọi M và E lần lượt là trung điểm của SC và AB. Tính khoảng cách từ điểm S đến mặt phẳng (MAB).
Giải:
Bài toán hoàn toàn được giải quyết nhanh gọn nếu các bạn học sinh mà cô Lý đang dạy đã học lớp 12.
Vì khi đó chúng ta còn 2 công cụ là ĐỔI ĐỈNH (Có ứng dụng tỉ số thể tích) và GẮN TOẠ ĐỘ OXYZ.
Nhưng do học sinh đang học 11 nên ta chỉ có thể dùng PP ĐỔI ĐIỂM như sau:
Thứ Tư, 20 tháng 8, 2014
Một bất đẳng thức đẹp...
Đề bài: (Câu hỏi của cô Phạm Thiên Lý hỏi trên facebook Trợ Giúp Toán Học)\[Cho\,\left\{ \begin{array}{l}
a + b + c = 3\\
a,b,c > 0
\end{array} \right..\,CMR:\frac{1}{{a + 3b}} + \frac{1}{{b + 3c}} + \frac{1}{{c + 3a}} \ge \frac{1}{{a + 3}} + \frac{1}{{b + 3}} + \frac{1}{{c + 3}}\left( * \right)\,\]
Giải:
Áp dụng Bất Đẳng Thức quen thuộc $\ \left( {x + y} \right)\left( {\frac{1}{x} + \frac{1}{y}} \right) \ge 4 \Leftrightarrow \frac{1}{x} + \frac{1}{y} \ge \frac{4}{{x + y}}\left( {x = y} \right)$ ta có:
Đọc tiếp
a + b + c = 3\\
a,b,c > 0
\end{array} \right..\,CMR:\frac{1}{{a + 3b}} + \frac{1}{{b + 3c}} + \frac{1}{{c + 3a}} \ge \frac{1}{{a + 3}} + \frac{1}{{b + 3}} + \frac{1}{{c + 3}}\left( * \right)\,\]
Giải:
Áp dụng Bất Đẳng Thức quen thuộc $\ \left( {x + y} \right)\left( {\frac{1}{x} + \frac{1}{y}} \right) \ge 4 \Leftrightarrow \frac{1}{x} + \frac{1}{y} \ge \frac{4}{{x + y}}\left( {x = y} \right)$ ta có:
Ứng dụng một bất đẳng thức quen thuộc.
Có những Bất đẳng thức đơn giản với 1 lời giải thật ngắn gọn nhưng hiệu quả của nó sẽ không dừng lại ở đó nếu ta biết vận dụng nó để sáng tạo và tìm lời giải cho các bài toán mới. Chuyên đề này đề cập đến một bất đẳng thức quen thuộc, đơn giản và một số bài toán áp dụng bất đẳng thức này.
Bài toán: Với hai số dương x và y ta có:
$\frac{1}{{x + y}} \le \frac{1}{4}(\frac{1}{x} + \frac{1}{y})$ (1)
Đẳng thức xảy ra khi $x =y$.
Bất đẳng thức (1) có nhiều cách chứng minh ở đây đưa ra hai cách chứng minh phổ biến nhất.
Tương giao đồ thị hàm số.
Đề bài: (Câu hỏi của bạn Mẫn Mạnh Mẽ hỏi trên facebook Trợ Giúp Toán Học)
Tìm m để đồ thị hàm số$y = \frac{{2x + 1}}{{x - 1}}\left( C \right)\,$ cắt đường thẳng $\ {d_m}:y = mx + 2 - m$ tại 2 điểm phân biệt A và B, sao cho chúng cách đều điểm D(2;-1).
Giải:
Hoành độ giao điểm của (C) và $\ {d_m}$ là nghiệm của phương trình:\[\begin{array}{l}
\frac{{2x + 1}}{{x - 1}} = mx + 2 - m \Leftrightarrow \left\{ \begin{array}{l}
g\left( x \right) = m{x^2} - 2mx + m - 3 = 0\\
x \ne 1
\end{array} \right.\\
\Rightarrow \exists \left\{ {A \ne B} \right\} = \left( C \right)\,\, \cap {d_m} \Leftrightarrow \left\{ \begin{array}{l}
{\Delta _g}^\prime > 0\\
g\left( 1 \right) \ne 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
3m > 0\\
- 3 \ne 0
\end{array} \right. \Leftrightarrow m > 0\,\left( * \right)\,
\end{array}\]
Đọc tiếp
Tìm m để đồ thị hàm số$y = \frac{{2x + 1}}{{x - 1}}\left( C \right)\,$ cắt đường thẳng $\ {d_m}:y = mx + 2 - m$ tại 2 điểm phân biệt A và B, sao cho chúng cách đều điểm D(2;-1).
Giải:
Hoành độ giao điểm của (C) và $\ {d_m}$ là nghiệm của phương trình:\[\begin{array}{l}
\frac{{2x + 1}}{{x - 1}} = mx + 2 - m \Leftrightarrow \left\{ \begin{array}{l}
g\left( x \right) = m{x^2} - 2mx + m - 3 = 0\\
x \ne 1
\end{array} \right.\\
\Rightarrow \exists \left\{ {A \ne B} \right\} = \left( C \right)\,\, \cap {d_m} \Leftrightarrow \left\{ \begin{array}{l}
{\Delta _g}^\prime > 0\\
g\left( 1 \right) \ne 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
3m > 0\\
- 3 \ne 0
\end{array} \right. \Leftrightarrow m > 0\,\left( * \right)\,
\end{array}\]
Thứ Hai, 18 tháng 8, 2014
Ngày mai bắt đầu từ hôm nay...
Đề bài: (Câu hỏi của bạn Black King hỏi trên facebook Trợ Giúp Toán Học)
Cho tứ diện đều ABCD, cạnh a. Điểm E thuộc AD( E không trùng A, D)
a, Xác định thiết diện của tứ diện cắt bởi mặt phẳng ($\alpha$) qua E, //AB,CD. Thiết diện là hình gì?
b, Gọi G, H lần lượt là trung điểm của AB, CD. Xác định giao điểm của GH với ($\alpha$)?
c, Xác định E thuộc AD sao cho diện tích thiết diện ở câu a đạt Max?
Giải:
a) $\ \left\{ \begin{array}{l}
E \in \left( \alpha \right)\\
AB//\left( \alpha \right)\\
CD//\left( \alpha \right)
\end{array} \right. \Rightarrow $Trong (ACD) dựng EM//CD(M thuộc CD) và trong (ABD) dựng EK//AB(K thuộc AB).
Khi đó: $\ \left( \alpha \right) \equiv \left( {MEK} \right).$
$\ \begin{array}{l}
\left\{ \begin{array}{l}
M \in \left( {MEK} \right) \cap \left( {ABC} \right)\\
EK//AB\\
EK \subset \left( {MEK} \right);\,AB \subset \left( {ABC} \right)
\end{array} \right.\\
\Rightarrow \left( {MEK} \right) \cap \left( {ABC} \right) = MN//AB\left( {N \in BC} \right)
\end{array}.$
Đọc tiếp
Cho tứ diện đều ABCD, cạnh a. Điểm E thuộc AD( E không trùng A, D)
a, Xác định thiết diện của tứ diện cắt bởi mặt phẳng ($\alpha$) qua E, //AB,CD. Thiết diện là hình gì?
b, Gọi G, H lần lượt là trung điểm của AB, CD. Xác định giao điểm của GH với ($\alpha$)?
c, Xác định E thuộc AD sao cho diện tích thiết diện ở câu a đạt Max?
Giải:
a) $\ \left\{ \begin{array}{l}
E \in \left( \alpha \right)\\
AB//\left( \alpha \right)\\
CD//\left( \alpha \right)
\end{array} \right. \Rightarrow $Trong (ACD) dựng EM//CD(M thuộc CD) và trong (ABD) dựng EK//AB(K thuộc AB).
Khi đó: $\ \left( \alpha \right) \equiv \left( {MEK} \right).$
$\ \begin{array}{l}
\left\{ \begin{array}{l}
M \in \left( {MEK} \right) \cap \left( {ABC} \right)\\
EK//AB\\
EK \subset \left( {MEK} \right);\,AB \subset \left( {ABC} \right)
\end{array} \right.\\
\Rightarrow \left( {MEK} \right) \cap \left( {ABC} \right) = MN//AB\left( {N \in BC} \right)
\end{array}.$
Dùng cái vặt vảnh, làm cái lớn...
Đề bài: (Câu hỏi của bạn EmYêu Toán hỏi trên facebook Trợ Giúp Toán Học)\[Cho\,\left\{ \begin{array}{l}
a,b,c > 0\\
ab + bc + ca \le abc
\end{array} \right..\,CMR:\frac{8}{{a + b}} + \frac{8}{{b + c}} + \frac{8}{{c + a}} \le \frac{{b + c}}{{{a^2}}} + \frac{{c + \,a}}{{{b^2}}} + \frac{{a + b}}{{{c^2}}} + 2\left( * \right)\]Giải:
Ta có: $\ \left\{ \begin{array}{l}
a,b,c > 0\\
ab + bc + ca \le abc
\end{array} \right. \Leftrightarrow 0 < \frac{1}{a} + \frac{1}{b} + \frac{1}{c} \le 1.$
Đọc tiếp
a,b,c > 0\\
ab + bc + ca \le abc
\end{array} \right..\,CMR:\frac{8}{{a + b}} + \frac{8}{{b + c}} + \frac{8}{{c + a}} \le \frac{{b + c}}{{{a^2}}} + \frac{{c + \,a}}{{{b^2}}} + \frac{{a + b}}{{{c^2}}} + 2\left( * \right)\]Giải:
Ta có: $\ \left\{ \begin{array}{l}
a,b,c > 0\\
ab + bc + ca \le abc
\end{array} \right. \Leftrightarrow 0 < \frac{1}{a} + \frac{1}{b} + \frac{1}{c} \le 1.$
PTLG đưa về PT tích.
Đề bài (Câu hỏi của bạn Minh Phương Ngô hỏi trên facebook Trợ Giúp Toán Học)
Giải phương trình: $\ \frac{{2\left[ {{{\left( {sin\,x - cos\,x} \right)}^2} + 2si{n^2}x} \right]}}{{1 + ta{n^2}x}} + sin\left( {x + \frac{\pi }{4}} \right) + cos\left( {3x - \frac{\pi }{4}} \right) = 2 + 2\,cos2x\left( * \right).$
Giải: Điều kiện $\ x \ne \frac{\pi }{2} + k\pi ,k \in Z.$
Đọc tiếp
Giải phương trình: $\ \frac{{2\left[ {{{\left( {sin\,x - cos\,x} \right)}^2} + 2si{n^2}x} \right]}}{{1 + ta{n^2}x}} + sin\left( {x + \frac{\pi }{4}} \right) + cos\left( {3x - \frac{\pi }{4}} \right) = 2 + 2\,cos2x\left( * \right).$
Giải: Điều kiện $\ x \ne \frac{\pi }{2} + k\pi ,k \in Z.$
Chủ Nhật, 17 tháng 8, 2014
Áp dụng BĐT phụ + Cauchy-Schwarz.
Đề bài: (Câu hỏi của bạn Nguyễn Hiếu hỏi trên facebook Trợ Giúp Toán Học)\[Cho\,\left\{ \begin{array}{l}
x,y,z > 0\\
x + y + z = 1
\end{array} \right..\,Min\,P = \frac{{{x^2}\left( {y + z} \right)}}{{yz}} + \frac{{{y^2}\left( {z + x} \right)}}{{zx}} + \frac{{{z^2}\left( {x + y} \right)}}{{xy}}\]Giải:
Áp dụng BĐT phụ thường gặp$\ \left( {a + b} \right)\left( {\frac{1}{a} + \frac{1}{b}} \right) \ge 4 \Leftrightarrow \frac{1}{a} + \frac{1}{b} \ge \frac{4}{{a + b}}\left( {a = b} \right)$ta có:\[\left\{ \begin{array}{l}
\frac{{{x^2}\left( {y + z} \right)}}{{yz}} = {x^2}\left( {\frac{1}{x} + \frac{1}{y}} \right) \ge \frac{{4{x^2}}}{{y + z}}\\
\frac{{{y^2}\left( {z + x} \right)}}{{zx}} = {y^2}\left( {\frac{1}{z} + \frac{1}{x}} \right) \ge \frac{{4{y^2}}}{{z + x}}\\
\frac{{{z^2}\left( {x + y} \right)}}{{xy}} = {z^2}\left( {\frac{1}{x} + \frac{1}{y}} \right) \ge \frac{{4{z^2}}}{{x + y}}
\end{array} \right. \Rightarrow P \ge 4\left( {\frac{{{x^2}}}{{y + z}} + \frac{{{y^2}}}{{z + x}} + \frac{{{z^2}}}{{x + y}}} \right) = 4Q\]
Đọc tiếp
x,y,z > 0\\
x + y + z = 1
\end{array} \right..\,Min\,P = \frac{{{x^2}\left( {y + z} \right)}}{{yz}} + \frac{{{y^2}\left( {z + x} \right)}}{{zx}} + \frac{{{z^2}\left( {x + y} \right)}}{{xy}}\]Giải:
Áp dụng BĐT phụ thường gặp$\ \left( {a + b} \right)\left( {\frac{1}{a} + \frac{1}{b}} \right) \ge 4 \Leftrightarrow \frac{1}{a} + \frac{1}{b} \ge \frac{4}{{a + b}}\left( {a = b} \right)$ta có:\[\left\{ \begin{array}{l}
\frac{{{x^2}\left( {y + z} \right)}}{{yz}} = {x^2}\left( {\frac{1}{x} + \frac{1}{y}} \right) \ge \frac{{4{x^2}}}{{y + z}}\\
\frac{{{y^2}\left( {z + x} \right)}}{{zx}} = {y^2}\left( {\frac{1}{z} + \frac{1}{x}} \right) \ge \frac{{4{y^2}}}{{z + x}}\\
\frac{{{z^2}\left( {x + y} \right)}}{{xy}} = {z^2}\left( {\frac{1}{x} + \frac{1}{y}} \right) \ge \frac{{4{z^2}}}{{x + y}}
\end{array} \right. \Rightarrow P \ge 4\left( {\frac{{{x^2}}}{{y + z}} + \frac{{{y^2}}}{{z + x}} + \frac{{{z^2}}}{{x + y}}} \right) = 4Q\]
Thứ Tư, 13 tháng 8, 2014
QHVG, góc giữa 2 mặt.
Đề bài: (Câu hỏi của bạn VerTu Motorbyke hỏi trên facebook cô Hà Nghĩa Phạm)
Cho hình chóp S.ABCD có đáy ABCD cạnh a,$SA = a\sqrt 3 $ và SA vuông góc với đáy ABCD. Gọi BM và DN là 2 đường cao của tam giác SBD. a) CMR: $\left( {AMN} \right) \bot \left( {SBC} \right).$ b) Tính $\widehat {\left( {\left( {SAC} \right),\left( {SBC} \right)} \right)}$
Giải:
$\ a)\,CMR:\left( {SBC} \right) \bot \left( {AMN} \right)\,\,\,\,\,.$
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD cạnh a,$SA = a\sqrt 3 $ và SA vuông góc với đáy ABCD. Gọi BM và DN là 2 đường cao của tam giác SBD. a) CMR: $\left( {AMN} \right) \bot \left( {SBC} \right).$ b) Tính $\widehat {\left( {\left( {SAC} \right),\left( {SBC} \right)} \right)}$
Giải:
$\ a)\,CMR:\left( {SBC} \right) \bot \left( {AMN} \right)\,\,\,\,\,.$
Thứ Hai, 11 tháng 8, 2014
HHGT liên quan đến đường tròn Euler.
Đề bài: (Câu hỏi của bạn Gly Ala Val hỏi trên facebook Trợ Giúp Toán Học)
Trong mặt phẳng với hệ toạ độ Oxy, cho tam giác ABC có trọng tâm G(1;1). Phương trình đường tròn đi qua trung điểm của các đọan BA, BC và chân đường cao hạ từ B xuống cạnh AC có phương trình x²+(y+1)²=4. Viết phương trình đường tròn ngoại tiếp tam giác ABC.
Giải:
Ta thấy ngay phương trình đường tròn đã cho chính là đường tròn Ơle đi qua 9 điểm:
- 3 trung điểm của 3 cạnh tam giác ABC.
- 3 chân đường cao xuất phát từ các đỉnh đến các cạnh đối diện của tam giác ABC.
- 3 trung điểm của các đoạn nối từ trực tâm đến các đỉnh của tam giác ABC.
Khi đó, gọi N là trung điểm của BC. Khi đó N thuộc đường tròn x²+(y+1)²=4.
Mặt khác, $\ \left\{ \begin{array}{l}
\overrightarrow {GA} = -2\overrightarrow {GN} \Rightarrow \exists V_{G\left( {1;1} \right)}^{k = -2}\left( N \right) = G\\
N \in {x^2} + {\left( {y - 1} \right)^2} = 4\left( {I\left( {0; - 1} \right),R' = 2} \right)
\end{array} \right.$\[ \Rightarrow A,B,C \in \left( O \right):\left\{ \begin{array}{l}
R = 2R' = 4\\
\overrightarrow {GO} = -2\overrightarrow {GI} \Leftrightarrow I\left( {3;5} \right)
\end{array} \right. \Rightarrow \left( {ABC} \right):{\left( {x - 3} \right)^2} + {\left( {y - 5} \right)^2} = 16\]
Trong mặt phẳng với hệ toạ độ Oxy, cho tam giác ABC có trọng tâm G(1;1). Phương trình đường tròn đi qua trung điểm của các đọan BA, BC và chân đường cao hạ từ B xuống cạnh AC có phương trình x²+(y+1)²=4. Viết phương trình đường tròn ngoại tiếp tam giác ABC.
Giải:
Ta thấy ngay phương trình đường tròn đã cho chính là đường tròn Ơle đi qua 9 điểm:
- 3 trung điểm của 3 cạnh tam giác ABC.
- 3 chân đường cao xuất phát từ các đỉnh đến các cạnh đối diện của tam giác ABC.
- 3 trung điểm của các đoạn nối từ trực tâm đến các đỉnh của tam giác ABC.
Khi đó, gọi N là trung điểm của BC. Khi đó N thuộc đường tròn x²+(y+1)²=4.
Mặt khác, $\ \left\{ \begin{array}{l}
\overrightarrow {GA} = -2\overrightarrow {GN} \Rightarrow \exists V_{G\left( {1;1} \right)}^{k = -2}\left( N \right) = G\\
N \in {x^2} + {\left( {y - 1} \right)^2} = 4\left( {I\left( {0; - 1} \right),R' = 2} \right)
\end{array} \right.$\[ \Rightarrow A,B,C \in \left( O \right):\left\{ \begin{array}{l}
R = 2R' = 4\\
\overrightarrow {GO} = -2\overrightarrow {GI} \Leftrightarrow I\left( {3;5} \right)
\end{array} \right. \Rightarrow \left( {ABC} \right):{\left( {x - 3} \right)^2} + {\left( {y - 5} \right)^2} = 16\]
VỎ=Tìm điểm, LÕI=Tương giao.
Đề bài: (Câu hỏi của bạn Hoả Long Natsu hỏi trên facebook Trợ Giúp Toán Học)
Cho hầm số$\ y = \frac{{{x^2}}}{{x - 1}}\left( C \right).$Tìm trên (C) cặp điểm đối xứng nhau qua đường thẳng $\Delta :y = x - 1.$.
Giải:
Gọi d là đường thẳng đi qua 2 điểm cần tìm. Do d vuông góc với $\Delta$ nên d:y = -x + m.
Hoành độ giao điểm của d và (C) là nghiệm của PT:$\ \frac{{{x^2}}}{{x - 1}} = - x + m \Leftrightarrow \left\{ \begin{array}{l}
x \ne 1\\
g\left( {x,m} \right) = 2{x^2} - \left( {m + 1} \right)x + m = 0
\end{array} \right.$
Đọc tiếp
Cho hầm số$\ y = \frac{{{x^2}}}{{x - 1}}\left( C \right).$Tìm trên (C) cặp điểm đối xứng nhau qua đường thẳng $\Delta :y = x - 1.$.
Giải:
Gọi d là đường thẳng đi qua 2 điểm cần tìm. Do d vuông góc với $\Delta$ nên d:y = -x + m.
Hoành độ giao điểm của d và (C) là nghiệm của PT:$\ \frac{{{x^2}}}{{x - 1}} = - x + m \Leftrightarrow \left\{ \begin{array}{l}
x \ne 1\\
g\left( {x,m} \right) = 2{x^2} - \left( {m + 1} \right)x + m = 0
\end{array} \right.$
Thứ Sáu, 8 tháng 8, 2014
Chiêu "BẤT bí di TUYẾN"
Đề bài: (Câu hỏi của bạn Drqm Sces hỏi trên facebook Trợ Giúp Toán Học)\[Cho\,\left\{ \begin{array}{l}
x,y > 0\\
x + y = 1
\end{array} \right..\,\,Min\,P = \frac{x}{{\sqrt {{y^2} + 1} }} + \frac{y}{{\sqrt {{x^2} + 1} }} = ?\]Phân tích:
Gặp bài toán rất đẹp thế này chúng ta có rất nhiều hướng giải, sau đây thầy sẽ phân tích các hướng và tính khả dụng của từng hướng đó:
- Hướng đi 1: Hướng này đa số được các bạn dùng nhờ tính đơn giản và dễ hiểu. Đó là việc rút x hoặc y từ điều kiện x + y = 1 và thế vào P xét hàm f(x) hay f(y) nhận được. Tuy nhiên, không phải mọi hàm số khi xét đều khả thi, đây là một trong số các hàm như vậy. Vì ở đây chứa nhiều điểm phức tạp: Tổng, các hàm phân thức, có chứa căn, không có quy luật căn...CANCEL.
- Hướng đi 2: Lượng giác hoá nhờ hệ thức x + y = 1. Việc này cũng được coi là quy về hàm một biến (biến góc) nhưng để biến đổi lượng giác và xét hàm lượng giác này cũng khá phức tạp vì tổng, các phân thức, chứa lượng giác, bậc cao...Chúng ta có thể giảm bậc nhưng lại đưa về hàm vô tỷ như hướng 1... CANCEL
- Hướng đi 3: Sử dụng PP chọn điểm rơi và cố gắng sử dụng các BĐT cổ điển (Cauchy, Cauchy-Schwarz). Cũng không thấy ổn, vì rằng rất khó tìm được lượng sử dụng thêm bớt và xuất hiện dấu hiệu sử dụng các BĐT trên...Thậm chí dễ dẫn đến xuất hiện dấu BĐT ngược chiều ở một bước nào đó... CANCEL.
- Hướng đi 4: Quy đồng lên, ép về tổng và tích của x và y, vận dụng x + y = 1 và đánh giá của xy để đưa về hàm f(t) trong đó t=xy. Nghe có vẻ dễ nhưng sẽ hơi dài và hàm f(t) nhận được xét nó không đơn giản đâu nhé, dù cho nó chỉ là một phân thức thôi nhưng tử và mẫu của nó thì lại là các hàm phức tạp nữa đấy...CANCEL.
Đọc tiếp
x,y > 0\\
x + y = 1
\end{array} \right..\,\,Min\,P = \frac{x}{{\sqrt {{y^2} + 1} }} + \frac{y}{{\sqrt {{x^2} + 1} }} = ?\]Phân tích:
Gặp bài toán rất đẹp thế này chúng ta có rất nhiều hướng giải, sau đây thầy sẽ phân tích các hướng và tính khả dụng của từng hướng đó:
- Hướng đi 1: Hướng này đa số được các bạn dùng nhờ tính đơn giản và dễ hiểu. Đó là việc rút x hoặc y từ điều kiện x + y = 1 và thế vào P xét hàm f(x) hay f(y) nhận được. Tuy nhiên, không phải mọi hàm số khi xét đều khả thi, đây là một trong số các hàm như vậy. Vì ở đây chứa nhiều điểm phức tạp: Tổng, các hàm phân thức, có chứa căn, không có quy luật căn...CANCEL.
- Hướng đi 2: Lượng giác hoá nhờ hệ thức x + y = 1. Việc này cũng được coi là quy về hàm một biến (biến góc) nhưng để biến đổi lượng giác và xét hàm lượng giác này cũng khá phức tạp vì tổng, các phân thức, chứa lượng giác, bậc cao...Chúng ta có thể giảm bậc nhưng lại đưa về hàm vô tỷ như hướng 1... CANCEL
- Hướng đi 3: Sử dụng PP chọn điểm rơi và cố gắng sử dụng các BĐT cổ điển (Cauchy, Cauchy-Schwarz). Cũng không thấy ổn, vì rằng rất khó tìm được lượng sử dụng thêm bớt và xuất hiện dấu hiệu sử dụng các BĐT trên...Thậm chí dễ dẫn đến xuất hiện dấu BĐT ngược chiều ở một bước nào đó... CANCEL.
- Hướng đi 4: Quy đồng lên, ép về tổng và tích của x và y, vận dụng x + y = 1 và đánh giá của xy để đưa về hàm f(t) trong đó t=xy. Nghe có vẻ dễ nhưng sẽ hơi dài và hàm f(t) nhận được xét nó không đơn giản đâu nhé, dù cho nó chỉ là một phân thức thôi nhưng tử và mẫu của nó thì lại là các hàm phức tạp nữa đấy...CANCEL.
Sử dụng liên tiếp BĐT Cauchy-Schwarz.
Đề bài: (Câu hỏi của bạn Thiện Tân Lê hỏi trên facebook Trợ Giúp Toán Học)\[Cho\,\left\{ \begin{array}{l}
0 < a,b,c \in R\\
a + b + c = 1
\end{array} \right..\,CMR:\,\frac{a}{{a + 6bc}} + \frac{b}{{b + 6ca}} + \frac{c}{{c + 6ab}} \ge 1\left( * \right)\]
Giải:
\[V{T_{\left( * \right)}} = P = \frac{a}{{a + 6bc}} + \frac{b}{{b + 6ca}} + \frac{c}{{c + 6ab}} = \frac{{{a^2}}}{{{a^2} + 6abc}} + \frac{{{b^2}}}{{{b^2} + 6abc}} + \frac{{{c^2}}}{{{c^2} + 6abc}}\] Áp dụng BĐT Cauchy-Schwarz ta có:
Đọc tiếp
0 < a,b,c \in R\\
a + b + c = 1
\end{array} \right..\,CMR:\,\frac{a}{{a + 6bc}} + \frac{b}{{b + 6ca}} + \frac{c}{{c + 6ab}} \ge 1\left( * \right)\]
Giải:
\[V{T_{\left( * \right)}} = P = \frac{a}{{a + 6bc}} + \frac{b}{{b + 6ca}} + \frac{c}{{c + 6ab}} = \frac{{{a^2}}}{{{a^2} + 6abc}} + \frac{{{b^2}}}{{{b^2} + 6abc}} + \frac{{{c^2}}}{{{c^2} + 6abc}}\] Áp dụng BĐT Cauchy-Schwarz ta có:
Thứ Năm, 7 tháng 8, 2014
Nhận dạng tam giác - Một dạng bài tập rất hay!
Đề bài: (Câu hỏi của bạn Gấu Trúc hỏi trên facebook Trợ Giúp Toán Học)
Tam giác ABC có đặc điểm gì nếu:$\frac{{{a^2} - {b^2}}}{{{a^2} + {b^2}}} = \frac{{\sin \left( {A - B} \right)}}{{\sin \left( {A + B} \right)}}.$
Giải:
Với dạng toán này các em phải sử dụng tốt 2 kĩ năng sau:
- Sử dụng tốt tất cả công thức lượng giác đã được học.
- Sử dụng tốt tất cả các hệ thức lượng trong tam giác thường tốt.
Đọc tiếp
Tam giác ABC có đặc điểm gì nếu:$\frac{{{a^2} - {b^2}}}{{{a^2} + {b^2}}} = \frac{{\sin \left( {A - B} \right)}}{{\sin \left( {A + B} \right)}}.$
Giải:
Với dạng toán này các em phải sử dụng tốt 2 kĩ năng sau:
- Sử dụng tốt tất cả công thức lượng giác đã được học.
- Sử dụng tốt tất cả các hệ thức lượng trong tam giác thường tốt.
Đăng ký:
Nhận xét (Atom)