"Ép" cái KHÓ về cái DỄ.

Đề bài: (Câu hỏi của bạn Thanh Tung hỏi trên facebook Trợ Giúp Toán Học)
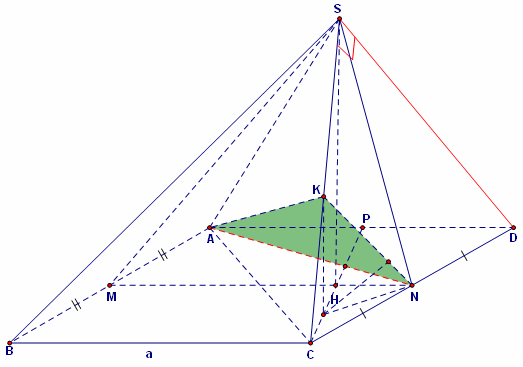
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Tam giác SAB đều. Tam giác SCD vuông cân tại S. N là trung điểm của cạnh CD.
a/ Tính thể tích hình chóp S.ABCD.
b/ Tính khoảng cách AN tới SD.
Giải:

Một bài toán khá hay nếu sử dụng công cụ hình học thuần túy. 

 a) Gọi M là trung điểm của AB ta có:$\left\{ \begin{array}{l}
MN \bot CD\\
SN \bot CD
\end{array} \right. \Rightarrow CD \bot \left( {SMN} \right).$
Trong (SMN), dựng SH vuông góc MN ta có:$SH \bot \left( {ABCD} \right).$
$SM = \frac{{a\sqrt 3 }}{2};MN = a;SN = \frac{a}{2} \Rightarrow M{N^2} = A{M^2} + S{N^2}.$

Khi đó tam giác SMN vuông tại S và ta có:$SH = \frac{{a\sqrt 3 }}{4} \Rightarrow MH = \frac{{3a}}{4} \Rightarrow \frac{{MH}}{{MN}} = \frac{3}{4}.$
$\Rightarrow {V_{S.ABCD}} = \frac{1}{3}.{a^2}.\frac{{a\sqrt 3 }}{4} = \frac{{{a^3}\sqrt 3 }}{{12}}.$

b) Gọi P là trung điểm của SC khi đó (SD)//(PAN) nên:

$\begin{array}{l}
\left\{ \begin{array}{l}
d\left( {AN,SD} \right) = d\left( {SD,(APN)} \right) = d\left( {D \to (APN)} \right)\\
CD \cap (APN) = N\left( {NC = ND} \right)
\end{array} \right.\\
 \Rightarrow d\left( {D \to (APN)} \right) = d\left( {C \to (APN)} \right)\left( 1 \right)
\end{array}.$
Trong (SHC) dựng PE//SH(E thuộc HC), khi đó E là trung điểm HC.
Gọi O là tâm của đáy, khi đó HO=HN và ta có: H thuộc CP và DQ (P và Q lần lượt là trung điểm của AD và BC).
Đến đây ta thấy một tính chất rất hay và quen thuộc, từng xuất hiện trong đề thi đại học là đoạn AN sẽ vuông góc với đoạn DQ tại giao điểm I của chúng (chứng minh không khó, bằng việc xét tam giác bằng nhau và cộng góc).
Lúc này ta có:$\left\{ \begin{array}{l}
EH = EC\\
ND = NC
\end{array} \right. \Rightarrow EN//HD \Rightarrow EN \bot AN.$
$\left\{ \begin{array}{l}
EN \bot AN\\
PE \bot AN
\end{array} \right. \Rightarrow AN \bot \left( {PEN} \right).$ Vậy trong (PEN) dựng EK vuông góc với PN ta được: $d\left( {E \to (PAN)} \right) = EK.$
$\begin{array}{l}
\left\{ \begin{array}{l}
CH \cap AN = G \Rightarrow CH \cap \left( {PAN} \right) = G\\
CH = \frac{{CP}}{2} \Rightarrow CE = \frac{{CP}}{4}\\
CG = \frac{{2CP}}{3}
\end{array} \right. \Rightarrow \frac{{CE}}{{CG}} = \frac{3}{8} \Rightarrow d\left( {C \to (PNA)} \right) = \frac{8}{3}d\left( {E \to (PNA)} \right) = \frac{8}{3}EK\left( 2 \right)\\
\frac{1}{{E{K^2}}} = \frac{1}{{E{P^2}}} + \frac{1}{{E{N^2}}} = \frac{4}{{S{H^2}}} + \frac{4}{{D{H^2}}} = \frac{4}{{S{H^2}}} + \frac{4}{{\sqrt {H{N^2} + N{D^2}} }} = \frac{{64}}{{3{a^2}}} + \frac{4}{{\sqrt {{{\left( {\frac{a}{4}} \right)}^2} + {{\left( {\frac{a}{2}} \right)}^2}} }} \Rightarrow EK = \frac{{\sqrt {30} }}{{32}}\left( 3 \right)
\end{array}.$
Từ (1), (2) và (3) ta có: $d\left( {AN,SD} \right) = \frac{8}{3}.\frac{{\sqrt {30} }}{{32}} = \frac{{\sqrt {30} }}{{12}}.$